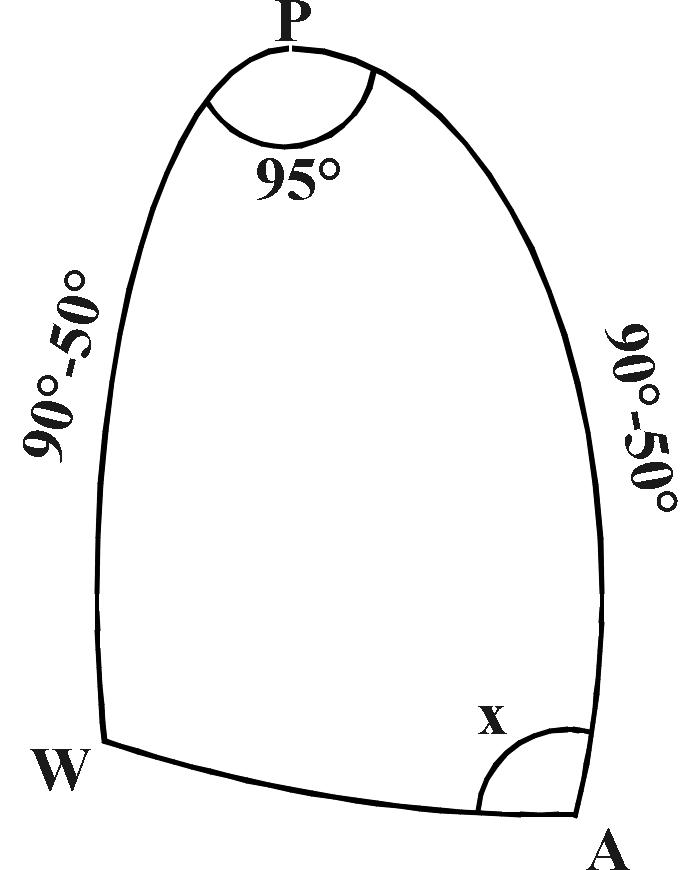
 Use
the cosine rule:
Use
the cosine rule:cos AW = cos WP cos AP + sin WP sin AP cos P
= cos240° + sin240° cos 95°
= 0.5508
So AW = 56.58°
= 3395 nautical miles
(This is 7% shorter than the route along a parallel of latitude).
Exercise:
Alderney, in the Channel
Islands, has longitude 2°W, latitude 50°N.
Winnipeg, in
Canada, has longitude 97°W, latitude 50°N.
How far apart
are they, in nautical miles, along a great circle arc?
 Use
the cosine rule:
Use
the cosine rule:
cos AW = cos WP cos AP + sin WP sin AP cos P
=
cos240° + sin240° cos 95°
= 0.5508
So AW = 56.58°
=
3395
nautical miles
(This is 7% shorter than the route along a
parallel of latitude).
If you set off from Alderney on
a great-circle route to Winnipeg,
in what direction (towards what
azimuth) would you head?
Use the sine rule:
sin A /
sin WP = sin P / sin WA
so sin x = sin 40° sin 95° / sin
56.58° = 0.77
so x = 50.1° or 129.9° .
Common sense says 50.1° (or
check using cosine rule to get PW).
Azimuth is measured
clockwise from north,
so azimuth is 360° - 50.1° = 309.9°
(Note that this is 40° north of the “obvious” due-west course.)
Back to "Spherical trigonometry".