Positional Astronomy:
Coordinate systems: the first equatorial or "HA-dec." system

We need a system of celestial coordinates which is fixed on the sky,
independent of the observer's time and place.
For this, we change the fundamental circle
from the horizon to the celestial equator.

The North Celestial Pole (NCP) and the South Celestial Pole (SCP)
lie directly above North and South Poles of Earth.
The NCP and SCP form the poles of a great circle on celestial sphere, analogous to the equator on Earth.
It is called the celestial equator and it lies directly above the Earth's equator.

Any great circle between the NCP and the SCP is a meridian.
The one which also passes through the zenith and the nadir
is "the" celestial meridian, or the observer's meridian.
(It is identical to the principal vertical.)
This provides our new zero-point;
in this case, we use the point where it crosses the southern half of the equator.

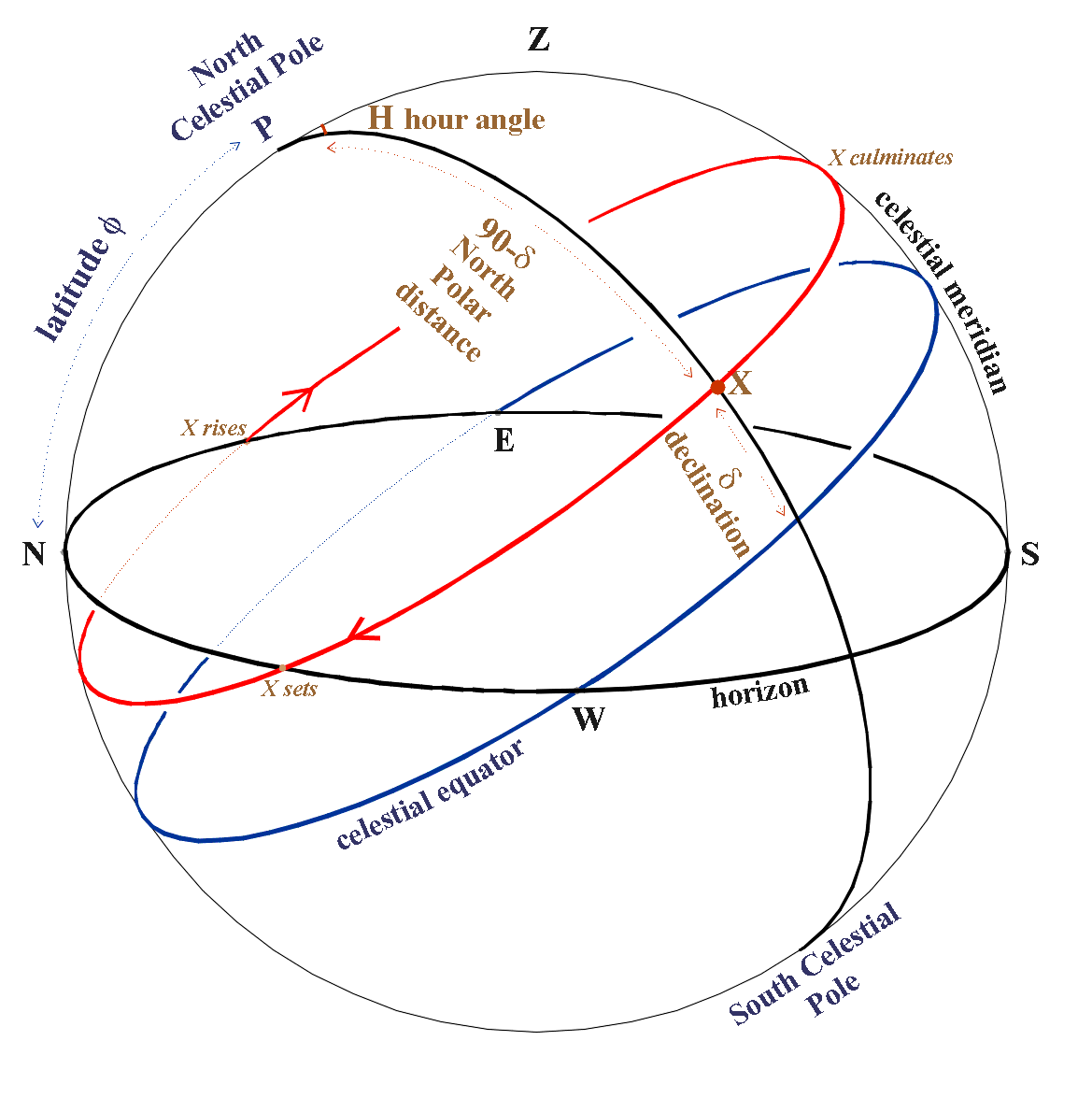
A typical star comes up over the horizon (rises) somewhere in the eastern sector;
it moves round to the right, climbing higher in the sky;
it reaches its highest point when it's due south, i.e. on the meridian;
it continues moving right, and sinking lower;
and it disappears below the horizon (sets) somewhere in the western sector.
(Note that this is only true in the northern hemisphere;
in the southern hemisphere, the star will move to the left,
and reach its highest point when it's due north.
In what follows, I assume we are in the northern hemisphere.)
The star's highest point, due south, is called (upper) transit or culmination.
The star will also cross the meridian again, in the opposite direction,
at the lowest point in its daily path.
This is called lower transit, and it occurs below the horizon unless the star is circumpolar.

Stars close to North Celestial Pole never set;
if a star's north polar distance is less than the altitude of the Pole,
then that star cannot reach the horizon.
These are defined as north circumpolar stars.
Similarly, stars close to the South Celestial Pole will never rise:
these are south circumpolar stars.
All others are equatorial stars, which rise and set.
The division between circumpolar and equatorial stars
depends on the altitude of the North Celestial Pole,
i.e. on the observer's latitude.

To fix the coordinates of an object X on the celestial sphere,
draw the meridian through X.
The declination δ of X is the angular distance
from the celestial equator to X,
measured from -90° at the SCP to +90° at the NCP.
Any point on celestial equator has declination 0°.
Alternatively, the North Polar Distance of X = 90° - δ.
Any two objects with the same declination lie on a parallel of declination.

The Hour Angle or HA (H) of object X
is the angular distance between the meridian of X and "the" celestial meridian.
It is measured westwards in hours, 0h-24h, since the Earth rotates 360° in 24 hours.

An object on the meridian (culminating) has H = 0h.
Its HA then steadily increases as the object moves westwards.
At lower transit, when it is due north (and possibly below the horizon), H = 12h.
At H = 23h, it is just one hour short of culminating again.

This system is still dependent on the time of observation,
but an object's declination generally doesn't change rapidly,
and its Hour Angle can be determined quite simply,
given the time and the location.
A telescope can be built on an equatorial mounting,
with its axis pointing at the NCP.
Once it is set on a star,
if the telescope rotates about its polar axis at the correct speed (15° per hour),
the star will stay in view.

Exercise:

The most northerly star of the Southern Cross, γ Crucis, has declination -57°.
At what latitude will it just be visible?

At what latitude will it pass directly overhead?

At what latitudes will it never set?

Click here for the answer.

Previous section: Coordinate systems: the horizontal or "alt-az" system
Next section: Coordinate systems: the second equatorial or "RA-dec" system
Return to index