Positional Astronomy:
Conversion
between horizontal and equatorial systems
{Note: If your browser does not distinguish
between "a,b" and "α, β" (the Greek letters
"alpha, beta")
then I am afraid you will not be able to make much sense of the
equations on this page.}
To convert between the horizontal and equatorial
coordinates for an object X,
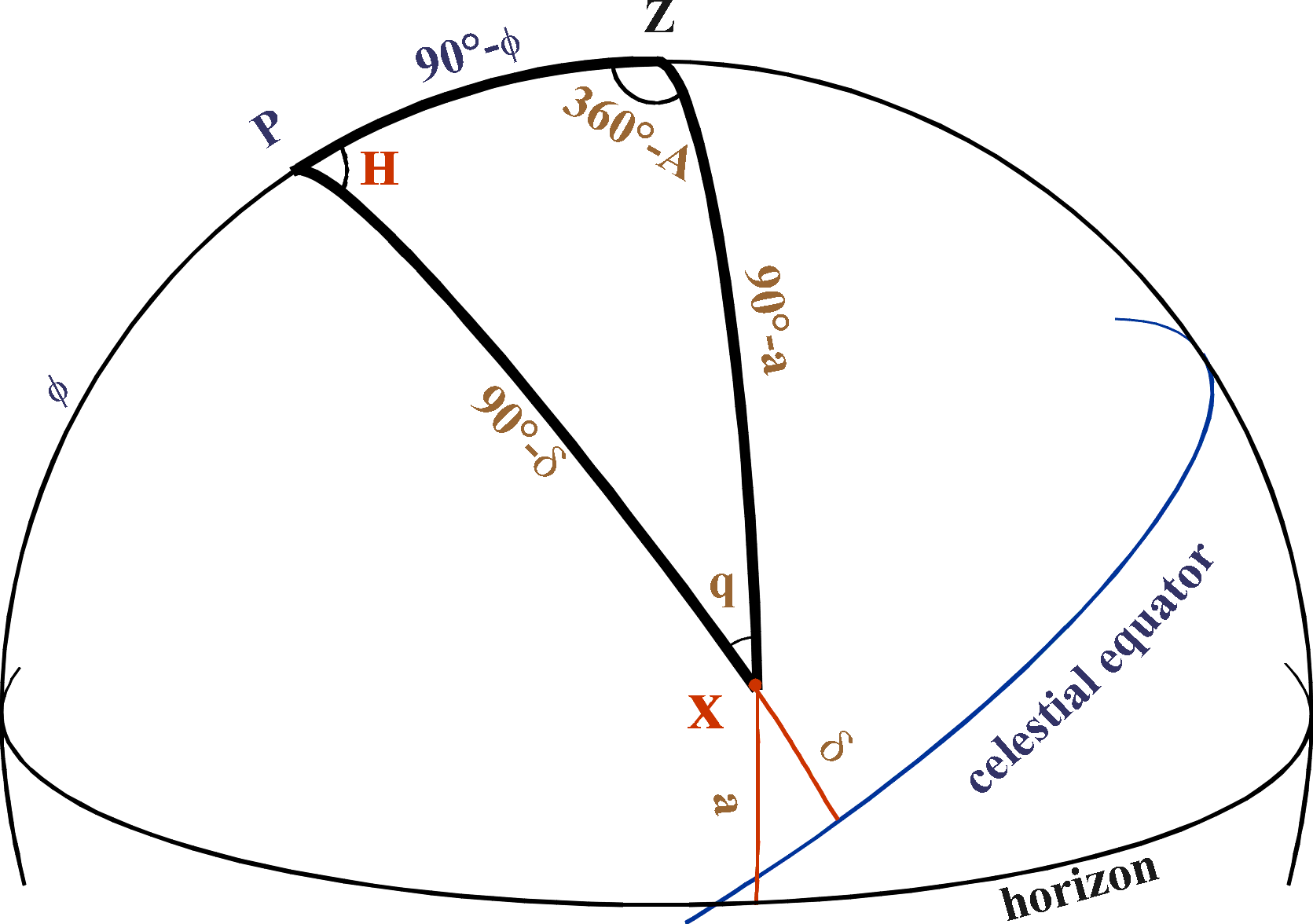
we use a spherical triangle often
called "The" Astronomical Triangle: XPZ,
where Z
is the zenith, P is the North Celestial Pole, and X is the object.
The sides of the triangle:
PZ is
the observer's co-latitude = 90°-φ.
ZX
is the zenith distance of X = 90°-a.
PX is
the North Polar Distance of X = 90°-δ.
The angles of the triangle:
The
angle at P is H, the local Hour Angle of X.
The
angle at Z is 360°-A, where A is the azimuth of X.
The
angle at X is q, the parallactic angle.
We assume we know the observer’s latitude φ
and the Local Sidereal Time LST.
(LST may be obtained, if
necessary, from Greenwich Sidereal Time and observer’s
longitude.)
To
convert from equatorial to horizontal coordinates:
Given RA α and
declination δ, we have
Local
Hour Angle H = LST - RA, in hours;
convert H to degrees (multiply
by 15).
Given H and δ, we
require azimuth A and altitude a.
By the cosine rule:
cos(90°-a) = cos(90°-δ)
cos(90°-φ) + sin(90°-δ)
sin(90°-φ) cos(H)
which
simplifies to:
sin(a) = sin(δ)
sin(φ) + cos(δ)
cos(φ) cos(H)
This gives us
the altitude a.
By the sine rule:
sin(360°-A)/sin(90°-δ)
= sin(H)/sin(90°-a)
which simplifies to:
- sin(A)/cos(δ)
= sin(H)/cos(a)
i.e. sin(A) = - sin(H) cos(δ)
/ cos(a)
which gives us the
azimuth A.
Alternatively, use the cosine rule again:
cos(90°-δ)
= cos(90°-φ) cos(90°-a) +
sin(90°-φ) sin(90°-a)
cos(360°-A)
which simplifies to
sin(δ)
= sin(φ) sin(a) + cos(φ)
cos(a) cos(A)
Rearrange to find A:
cos(A) = { sin(δ)
- sin(φ) sin(a) } / { cos(φ)
cos(a) }
which again gives us
the azimuth A.
Here
are all the equations together:
H = t -
α
sin(a)
= sin(δ) sin(φ)
+ cos(δ) cos(φ)
cos(H)
sin(A) = -
sin(H) cos(δ) / cos(a)
cos(A) =
{ sin(δ) - sin(φ)
sin(a) } / { cos(φ) cos(a) }
Now for the inverse problem:
to
convert from horizontal to equatorial coordinates:
Given φ, a and A,
what are α and δ?
Start by using the cosine rule to get δ,
as shown above:
sin(δ) =
sin(a)sin(φ) + cos(a) cos(φ)
cos(A)
We can now use the sine rule to get H, using the same
formula as above:
sin(H) = - sin(A) cos(a) / cos(δ)
Or use the cosine rule instead:
sin(a) = sin(δ)sin(φ)
+ cos(δ) cos(φ)
cos(H)
and rearrange to find H:
cos(H) = { sin(a) - sin(δ)
sin(φ) } / cos(δ)
cos(φ)
Having calculated H, ascertain the Local Sidereal
Time t.
Then the R.A. follows from
α
= t – H .
Here are all the equations together:
sin(δ)
= sin(a)sin(φ) + cos(a) cos(φ) cos(A)
sin(H) = - sin(A) cos(a) / cos(δ)
cos(H) = { sin(a) - sin(δ) sin(φ)} / cos(δ) cos(φ)
α = t – H
Exercise:
Prove that the celestial
equator cuts the horizon at azimuth 90° and 270°,
at any
latitude (except at the North and South Poles).
At what angle does the
celestial equator cut the horizon, at latitude φ
?
Click here
for the answer.
Previous section:
Sidereal time
Next
section: Galactic coordinates
Return
to index
